|
Home->‹bersicht
|
|
Puzzeln mit Neuronenvon Katja Miller mit Sebastian Hellberg |

|
|
Einleitung Theorie Modell Implementierung Quellen |

|
Einleitung | |||||
 Skizze des Zellkörpers einer Nervenzelle |
Um Nervensysteme, z.B. das Gehirn, besser zu verstehen, versucht man in der aktuellen Forschung, die Funktion von Nervenzellen (Bild links) zu simulieren. Für eine solche Simulation werden jedoch normalerweise sehr detaillierte Daten benötigt. Es muss aber möglich sein mit wenigen Daten ebenfalls zu den gesuchten Netzwerken zu gelangen, indem man Nervenzellen virtuell wachsen lässt - ähnlich dem natürlichen Wachstum. | ||||
| Für dieses stehen lediglich die Informationen aus der DNS zur Verfügung. Auf dieser Basis kann ein geeignetes Modell entwickelt werden, dass die virtuelle Erstellung neuer Netzwerke mit vorgegebenen Eigenschaften ermöglicht. |
Nervensystem |
||||
| |||||
Theorie | |||||
| Nervenzellen bilden während ihres Wachstums eine verzweigte Baumstruktur aus (Bild rechts: Pyramidenzelle). Diese Struktur ist für verschiedene Zelltypen charakteristisch. |
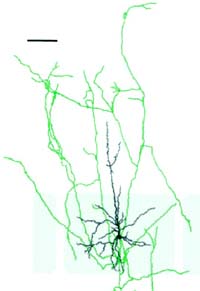 Pyramidenzelle aus dem Barrel Kortex der Ratte [5, S.8, Fig.6] |
||||
Wachstum |
Sie entsteht zum einen durch ungerichtetes Längenwachstum, zum anderen durch Strukturen und Stoffverteilungen in der Umgebung, die Stoffgradienten bilden. | ||||
| Außerdem ist die Struktur eines Nervensystems nicht statisch, sondern verändert sich abhängig von Erfahrungen, den Lebensbedingungen und dem Alter. Dieser Prozess ermöglicht ständiges Lernen und Anpassung an neue Bedingungen. |
Struktur |
||||
| |||||
Modell | |||||
| Die Struktur von Nervenzellen lässt sich mit Fraktalen (Bild rechts) modellieren (Schierwagen, 1987). Die Form der Fraktale wird durch die Vorgaben für Astlängen und Verzweigungswinkel gesteuert. |
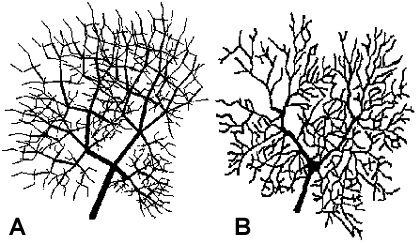 Fraktales Modell (A) und die original Purkinjezelle (B) eines Meerschweinchens (Pellionisz, 1989) |
||||
Wachstum |
|||||
| Die so entstehenden Fraktale bilden das ungerichtete Wachstum nach. Die Gradienten können durch Dichtefunktionen abgebildet werden, die als Wahrscheinlichkeit für eine Verzweigung oder ein Astende interpretiert werden. Alle für diese Modellierung benötigten Daten können schon aus wenigen 2D-Abbildungen von Nervenzellen gewonnen werden. Je mehr Bilder und Daten zur Verfügung stehen, desto genauer wird das Modell. | |||||
3D-Dichte |
2D-Abbildungen |
3D-Fraktal |
|||
| |||||
Implementierung | |||||
|
Die 3D-Dichte (Bild unten, C) kann aus den Verteilungen (A) der Punkte in den Abbildungen bestimmt werden, indem nach einer Dichte
gesucht wird, die zu der geschätzten durchschnittlichen Verteilung (B) passt.
Um die 3D-Dichte zu erhalten, wird angenommen, dass diese sich aus der Überlagerung dreidimensionaler
Gaußscher Dichtefunktionen
darstellen lässt. Passende Parameter können mit einem
genetischen Algorithmus gefunden werden
Zusätzlich werden eine solche Verteilung auch als Aufsicht benötigt oder es muss Rotationssymmetrie um die Hochachse
angenommen werden. |
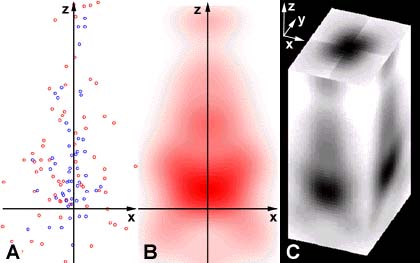 A: Verzweigungen (blau) und Astenden (rot) von Pyramidenzellen B: Geschätzte durchschnittliche Verteilung der Astenden in 2D und C: berechnete Dichte in 3D 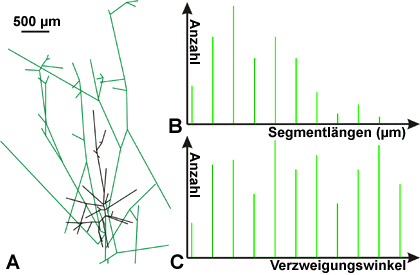 A: Vektorisierte Baumstruktur einer Pyramidenzelle (Dendriten schwarz, Axon grün) B: Verteilung der Längen der Astabschnitte C: Verteilung der Verzweigungswinkel |
||||
Modellannahmen |
|||||
| Auch für die Fraktale, die die Nervenzellen abbilden sollen, müssen Parameter gefunden werden. Dazu werden die zuerst zufällige Parameter mit der Monte-Carlo Methode eingegerenzt. Zu jeden Parametersatz kann dann überprüft werden, wie gut die berechneten Nervenzellen zu den Original-Abbildungen passen. | |||||
| |||||
Quellen | |||||
|
[1] C Koch, I Segev: "Methods in Neuronal Modeling - From Synapses to Networks" in TJ Sejnowski, TA Poggio (Hrsg): "Computational Neuroscience", First MIT Press Paperback Edition 1991, Copyright 1989 MIT [2] P Dayan, LF Abbott: "Theoretical Neuroscience - Computational and Mathematical Modeling of Neural Systems" in TJ Sejnowski, TA Poggio (Hrsg): "Computational Neuroscience", MIT Press, Copyright 2001 MIT [3] M Maravall, IYY Koh, WB Lindquist, K Svoboda: "Experience-dependent Changes in Basal Dendritic Branching of Layer 2/3 Pyramidal Neurons During a Critical Period for Developmental Plasticity in Rat Barrel Cortex", Cerebral Cortex June 2004; 14:655-664 [4] JK Pasternak, TA Woosley: "The number, size and spatial distribution of neurons in lamina IV of the mouse SmI neocortex", 1975; J. Comp. Neurol. 160, 291-306 [5] J Lübke, V Egger, B Sakmann, D Feldmeyer: "Columnar Organization of Dendrites and Axons of Single and Synaptically Coupled Excitatory Spiny Neurons in Layer 4 of the Rat Barrel Cortex", July 15, 2000; The Journal of Neuroscience , 20(14):5300-5311 [6] M Brecht, B Sakmann: "Dynamic representation of whisker deflection by synaptic potentials in spiny stellate and pyramidal cells in the barrels and septa of layer 4 rat somatosensory cortex", 2002; originally published online Jun 28, 2002; J Physiol 543, 49-70 [7] D Feldmeyer, J Lübke, RA Silver, B Sakmann: "Synaptic connections between layer 4 spiny neurone- layer 2/3 pyramidal cell pairs in a juvenile rat barrel cortex: physiology and anatomy of interlaminar signalling within a cortical column", 2002; J Physiol 538;803-822 [8] KJ Bender, J Rangel, DE Feldman: "Development of Columnar Topography in the Excitatory Layer 4 to Layer 2/3 Projection in Rat Barrel Cortex", September 24, 2003; The Journal of Neuroscience, 23(25):8759-8770, 8759 [9] C Tailby, LL Wright, AB Metha, MB Calford: "Activity-dependent maintenance and growth of dendrites in adult cortex", March 22, 2005; PNAS, vol. 102 no. 12, 4631-4636 [10] Y Wang, M Toledo-Rodriguez, A Gupta, C Wu, G Silberberg, J Luo, H Markram: "Anatomical, physiological and molecular properties of Martinotti cells in the somatosensory cortex of the juvenile rat", 2004; J Physiol 561.1, pp 65-90 [11] D Feldmeyer, B Sakmann: "Synaptic efficacy and reliability of excitatory connections between the principal neurones of the input (layer 4) and output layer (layer 5) of the neocortex", 2000; J Physiol 525;31-39 [12] CCH Petersen, B Sakmann: "The Excitatory Neuronal Network of Rat Layer 4 Barrel Cortex", October 15, 2000; The Journal of Neuroscience, 20(20):7579-7586 [13] CCH Petersen and B Sakmann: "Functionally Independent Columns of Rat Somatosensory Barrel Cortex Revealed with Voltage-Sensitive Dye Imaging", November 1, 2001; The Journal of Neuroscience, 21(21):8435-8446 [14] QQ Sun, JR Huguenard, DA Prince: "Barrel Cortex Microcircuits: Thalamocortical Feedforward Inhibition in Spiny Stellate Cells is Mediated by a Small Number of Fast-Spiking Interneurons", January 25, 2006; The Journal of Neuroscience, 26(4):1219-1230, 1219 [15] D Feldmeyer, J Lübke and B Sakmann: "Efficacy and connectivity of intracolumnar pairs of layer 2/3 pyramidal cells in the barrel cortex of juvenile rats", DOI: 10.1113/jphysiol.2006.105106 published online Jun 22, 2006; J Physiol [16] D Schubert, R Kötter K Zilles, HJ Luhmann, JF Staiger: "Cell Type-Specific Circuits of Cortical Layer IV Spiny Neurons", April 1, 2003; The Journal of Neuroscience, 23(7):2961-2970, 2961 [17] D Schubert, JF Staiger, N Cho, R Kötter, K Zilles, HJ Luhmann: "Layer-Specific Intracolumnar and Transcolumnar Functional Connectivity of Layer V Pyramidal Cells in Rat Barrel Cortex", May 15, 2001; The Journal of Neuroscience, 21(10):3580-3592 [18] ID Manns, B Sakmann M Brecht: "Sub- and suprathreshold receptive field properties of pyramidal neurons in layers 5A and 5B of rat somatosensory barrel cortex", 2004; J. Physiol 556.2, pp 601-622 [19] Y Wang, A Gupta, M Toledo-Rodriguez, CZ Wu, H Markram: "Anatomical, physiological and molecular properties of Nest Basket cells in the Developing Somatosensory Cortex", Apr 2002; Cerebral Cortex, 12:395-410; 1047-3211/02 [20] HAK Masterbroek, JE Vos: "Plausible Neural Network for Biological Modelling", Kluwer Academic Publishers, 2001 [21] M Abeles: Corticonics: "Neural circuits of the cerebral cortex", Cambridge University Press, 1991 [22] F. Ventriglia: "Neural modeling and neural networks", Pergamon Press, 1994 [23] RJ MacGregor: "Neural and Brain Modeling", in RF Thompson: "Neuroscience: a series of Mongraphes and Texts", Academic Press, Inc., 1987 [24] "Neurowissenschaft: Vom Molekül zur Kognition", Dudel (Hrsg), Springer-Verlag, Berlin, 2001, 2. Auflage [25] H. Hanser, C. Scholtyssek (Red): "Lexikon der Neuronwissenschaft: in vier Bänden", Spektrum akademischer Verlag, 2000 [26] Bronsten: "Taschenbuch der Mathematik", Verlag Harri Deutsch, 4. überarbeitete und erweiterte Auflage, 1999 | |||||
| |||||